Finite and Algorithmic Model Theory

Summary

Finite and Algorithmic Model Theory research revolves around the study of the expressive power of various logics on finite and finitely presented structures, and the connections between this and different computational models and mathematical formalisms.

The methods and tools of finite and algorithmic model theory (FAMT) have played an active role in the development of several areas of computer science. Finite or finitely representable structures are those that serve as inputs to computation, and the study of the expressive power of logical languages on such structures has led to fundamental insights in diverse areas, including database theory, computational complexity, random structures and combinatorics, verification, automata theory, proof complexity, and algorithmic game theory.

Over the past four decades FAMT has established itself as a rich research field with a strong and evolving community of researchers with a shared agenda. Much of the progress can be traced to the regular meetings of the community: the last such meeting was at Dagstuhl in 2017, and before that at Les Houches in 2012.

The principal goals of this seminar included:

1. To identify fresh challenges in FAMT arising from some of the main application areas as well as newly emerging ones.
2. To make connections between core research in FAMT and other subfields of theoretical computer science, such as the theory of combinatorial and continuous optimization algorithms, and the theory of homomorphism counts and limit structures.
3. To transfer knowledge from emerging techniques in core FAMT back to the connected subfields and application areas.
4. To strengthen the research community in FAMT, especially by integrating younger members into it.
5. To provide continuity for what has been a successful model of regular seminars for building and consolidating the productive research community in FAMT.

One of the main goals of this Dagstuhl Seminar was to capitalize on the progress and the potential impact of some of the latest developments in FAMT and related areas. Such developments include:

• The recently established connections between symmetric models of classical computation and bounded-variable counting logics. The symmetric counterparts of classical models of computations include threshold circuits, linear and semidefinite programs, and algebraic circuits. These new results have already been used to establish new upper and lower bounds for large families of algorithms by FAMT tools.
• The theories of homomorphism counts and limit structures in combinatorics. A recent trend of work establishes that distinguishing the structures by the number homomorphisms they admit from certain classes of patterns, or to certain classes of patterns, is a fruitful alternative to distinguishing them by the logic formulas they satisfy.
• Enumeration and counting methods including their use in database query processing, among others. One of the goals of this line of research is to understand and classify the logical queries for which it is possible to compute a compact representation of the output from which the query results can be obtained, efficiently, and on demand.

Organization and Activities

The organizers developed a schedule consisting of a number of invited survey talks, a number of talks focused on regular contributions proposed by participants, and an open problem session.

The seminar took place in person at Dagstuhl, with essentially all talks (except one) delivered by speakers attending Dagstuhl in person. The timing of the seminar coincided with the height of the Covid Omicron wave in Germany and Europe. This resulted in a number of late covid-related cancellations. Some talks, including invited talks, had to be cancelled, and the total number of participants (24) was fewer than originally planned.

Outcomes

Despite the many organizational challenges presented by the covid surge around the time of the workshop, the seminar was highly stimulating and surprisingly successful for those who were able to attend, and achieved many of our goals. (And thankfully there were no cases of covid during the seminar among those who did attend in person.)

The final program included invited tutorial talks by Martin Grohe on homomorphism counts (delivered online, to an in person audience at the workshop, due to a last minute cancellation for Grohe caused by COVID), David Roberson I and II on quantum isomorphism and its connection to homomorphism counting. These and other related talks at the seminar highlighted the exciting ongoing work aimed at delineating the power of homorphism counting on various classes of graphs and structures, with surprising connections to other areas of mathematics.

Another invited talk was by Albert Atserias on symmetric computation and descriptive complexity (replacing a last minute cancellation), highlighted the exciting recent developments at the intersection of FAMT and combinatorial optimization. Another invited talk on query enumeration also had to be cancelled due to COVID. The full schedule including all the other talks of the Seminar can be found in the adjoined table.

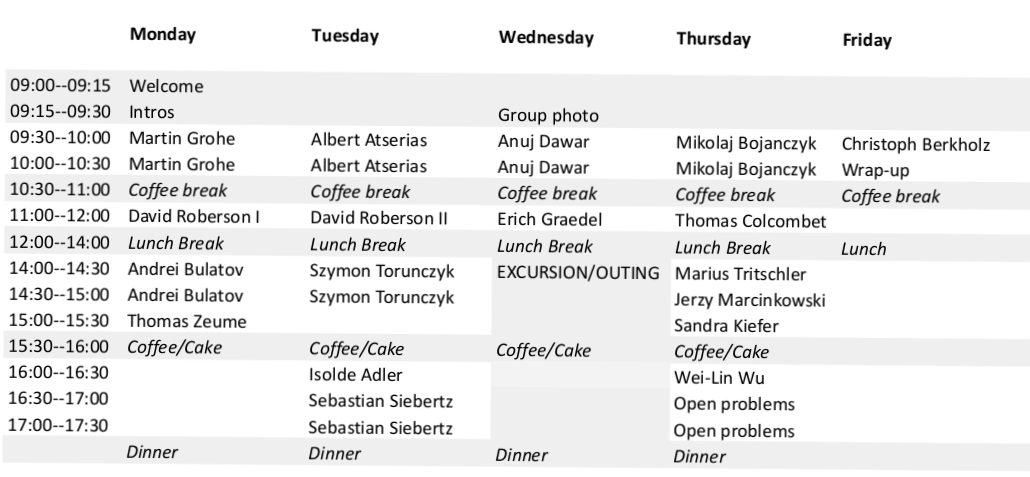
One of the traditions of the series of workshops on Finite and Algorithmic Model Theory is to have a session in which some of the attendants present open problems and directions for further research. In this occasion, an hour of the afternoon of Thursday was devoted to such a session. A couple of days earlier we made a public call for presentations of open problems. Volunteers would write down their name on an easel pad. By Thursday, three volunteers came forward who gave 10 minute presentations (aprox.) of their proposals.

First, Erich Graedel presented an open problem on the topic of his earlier talk on Wednesday. Shortly put, the open problem asks to develop a proof theory for the emerging field of semiring semantics for logic formulas. The motivation comes from its potential applications in database theory and game analysis. Second, Isolde Adler presented an open problem on a topic covered in an earlier talk by Torunczyk. In brief, the open problem asks to study the relationships between the various notions of model-theoretic stability for classes of hypergraphs and more general relational structures. Third, Kousha Etessami gave a short talk on his recent work on applications of Tarski's Fixed-Point Theorem to economic game theory. In a nutshell, the question asks how much faster can one compute an arbitrary fixed-point of a monotone operator on a grid lattice than it takes to compute the least or greatest fixed-point by the standard iteration method. A detailed exposition of this open problem and its motivations can be found in a later section of this report. Finally, during his talk on Tuesday, Albert Atserias announced an open problem related to the optimal hardness of approximating the minimum vertex cover on graphs. Since it was presented earlier during a talk, this open problem was not presented during the session. A detailed description of this open problem appears also in a later section of this report.

Overall, the organizers regard the seminar as a resounding success despite the difficult circumstances, and judging by the very positive feedback from participants, they agreed. We look forward to the next meeting of the FAMT community, hopefully within a few years, whether at Dagstuhl or elsewhere.

The organizers are grateful to the Scientific Directorate of the Center for its support of this workshop and the staff of Schloss Dagstuhl for their organisation of our stay (including regular covid testing) and their hospitality, despite the many challenges posed by covid.